どうもこんにちわ 国家一級整備士学科試験に出題されるテスタの内部抵抗の問題の解説をしていきます。

仕事をしながら独学で一級整備士試験に合格した私がそのお悩み解決へのお手伝いをします。
具体的な問題の内容は
オームの法則を用いた計算問題です。
整備士の実務でオームの法則を使うことはあまり多くないかと思いますので忘れている人も多いかと思います。ですが毎年この問題は出題されている傾向にあります。
理解して計算問題を解いていきたい・・・ところなのですが・・参考書通りに計算を解いていくととても時間がかかります!!
私自身も最初は参考書の計算方法で問題を解いていたのですが時間がかかりすぎてしまい他の問題が終わらないこともしばしばありました。
だから
「計算問題を最後に解こう」
という考えになりがちですが、そうではなく、最短の計算手順を覚えて素早く解いていきたいという考えに至り皆様にも解いてもらいたいとの気持ちからこの記事を書いてみました。
※なお、これは私が自己流で解いている方法なのでもっと早い方法はあるかと思います。なのでそちらも踏まえて参考にしていただければと思います。
テスタ内部抵抗の計算問題とはどんな問題?
スポンサーリンク
平成30年3月に出題された問題を例にすると
という問題です。
過去問の傾向は問題の内容は同じで電源電圧、抵抗値、内部抵抗、の数字が変えてあるだけの問題となります。
電圧計を接続すると電圧計の仕様で中に大きな内部抵抗と呼ばれる抵抗が入っています。この抵抗が並列に接続されますので僅かながら電圧計の大きな内部抵抗でも電圧を消費してしまいテスタの表示値が少し変わってしまうよーという問題内容です。
ですが問題を解く上には計算ができれば理解をしなくても問題ないと思います。
テスタ内部抵抗を回路図にしてみてみる
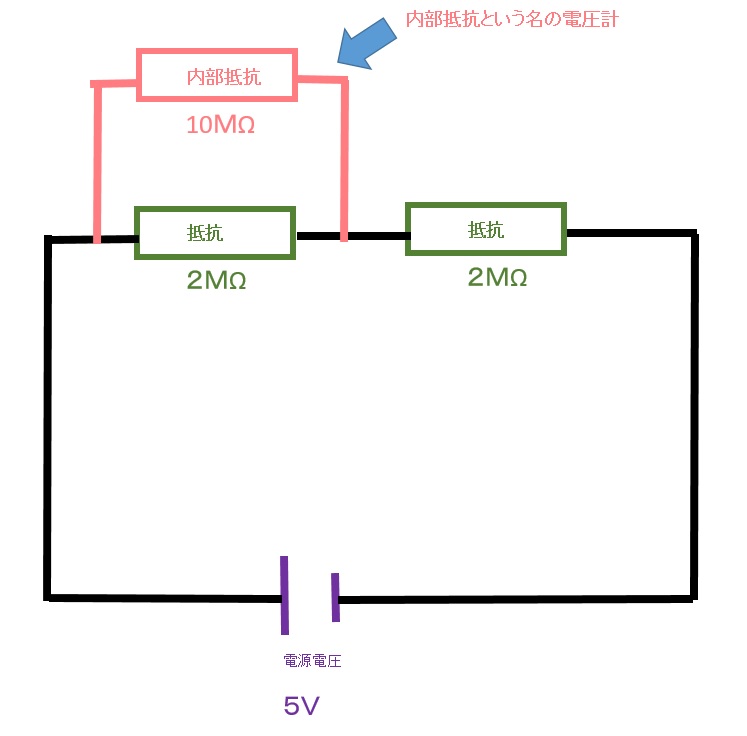
先ほどの平成30年3月出題された問題を回路図にしてみます。
電源電圧が5Vで、抵抗値2MΩの抵抗2個を直列に接続した回路において、片方の抵抗の両端に内部抵抗10MΩのテスタ(電圧計)を接続したとき計算で求められるテスタの表示値は約2.2727Vになる。
問題の内容を色分けをして回路図にしてみました。
ピンク抵抗にかかる電圧はいくつでしょうか?
というのがこの問題です。
あとはオームの法則を用いて計算をしていきます。
オームの法則の基礎
計算する上でオームの法則を最低限理解しないと解けませんのでこの問題に解く上で必要な法則を書きます。
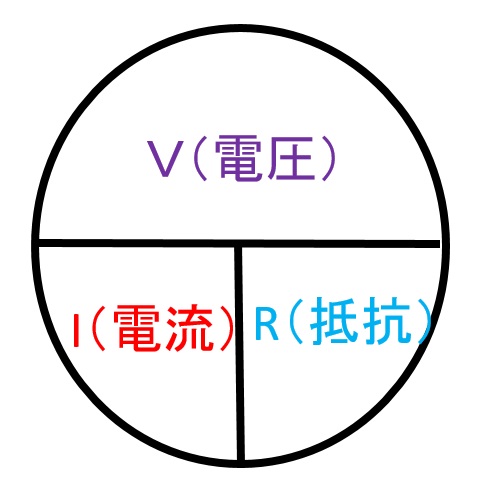
まずオームの法則基本中の基本
電流=電圧÷抵抗
抵抗=電圧÷電流
という計算方式で各々求めることができます。
電圧、電流、抵抗は特徴がありそこも超簡単に触れていきます。(がっつり触れると記事の内容が変わるほど深いため)
電圧の特徴
・プラスとマイナスとの電位差で電圧値がでる
・並列抵抗には同じ電圧がかかる
・電源の電源側では電源電圧の電圧が、アース側だと抵抗で電圧がすべて消費され0Vの電圧になる
・断線時などの回路不成立時は電源電圧が断線箇所までくる
電流の特徴
・直列回路時は同じ電流値が最初から最後まで流れる。
・並列回路時は並列回路の部分で分流して電流が流れる。(川の流れのイメージ)
抵抗の特徴
・直列の合成抵抗は足せばok
・並列の合成抵抗は2つの合成抵抗を和分の積という求め方で求めることができる(この先で説明します)
・直列と並列の合成抵抗があった場合並列の合成抵抗から計算をする
並列の合成抵抗の計算のやり方
スポンサーリンク
テスタの内部抵抗の問題を解くにあたり合成抵抗を素早く出すことが早く問題を解く近道になりますので直列の抵抗は足せばよいだけなので並列の合成抵抗の解き方をまず覚えましょう。
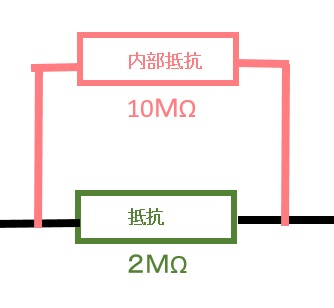
過去問での並列の合成抵抗は10MΩと2MΩとなります。
この2つの抵抗を合体させます。
やり方は先ほど抵抗の特徴で書きました和分の積という法則を使います。
具体的な数字を入れると・・
となり20M÷12M=1.666・・
合成抵抗は1.666MΩとなります。
10×2と10+2という計算は暗算でできるかと思いますので電卓では20÷12のみを行えばすぐに並列の合成抵抗が求めることができます。
テスタ内部抵抗を解く手順
1、回路図を書く(メモする)
まずは問題の傾向はほとんど変わらず数字のみが変化するので回路図をメモします。
最初のうちは上記のようにしっかりした回路図を書いたほうが分かりやすいでしょうが慣れてくると数字のみをメモするだけで問題が解けるようになります。
ちなみに私はこのくらいのメモで問題を解いていました。
2、合成抵抗を計算する
上記でも書きましたがまずは並列の抵抗を計算し、そこに直列の合成抵抗を足して回路全体の合成抵抗をだします。
これも上記の通り和分の積で並列の合成抵抗を計算し(1.66MΩ)そこに直列の2MΩを足して(1.66+2)3.66MΩという流れになります。
私のメモだとこんな感じ
3、電流を出す
合成抵抗がでたら今度は電流をだします。
出し方はオームの法則で電圧÷抵抗で出すことができます。
5V÷3.66Ω=1.363A
※ここであえてMΩ(メガオーム)の概念を消し去ってください。MΩで計算をすると電流が小数点まみれの数字がでてしまいます。この後電圧を計算しまする時にまた抵抗がでてきてMΩを考えなくても答えは変わりません。
4、答えの電圧を出す
回路全体の電流がでたらこの電流と2、で計算を行った並列抵抗の合成抵抗を掛けると電圧計の電圧を導き出すことができます。
テスタの表示値(電圧)=
1.363A ×1.666Ω
=2.27V
となり答えは正となります。
※割り切れない部分をどこで切るかによって若干数字が変わります。
まとめ

計算だけで考えると4つです。
2.回路全体の合成抵抗をだす
3.回路全体の電流をだす
4. 1.と3.を掛ける
これだけを行えば問題集にあるような分数で長々式を書く必要もなくなるかと思います。
近年の問題は時間がかかる問題がとても増えていて時間内に終わらなかったという声をよく聞きます。
そういう意味でも計算問題は時間を掛けずにスムーズに行えるように勉強を頑張りましょう^^
これから国家一級整備士を目指す方への少しでもお手伝いができれば幸いです。
おわり



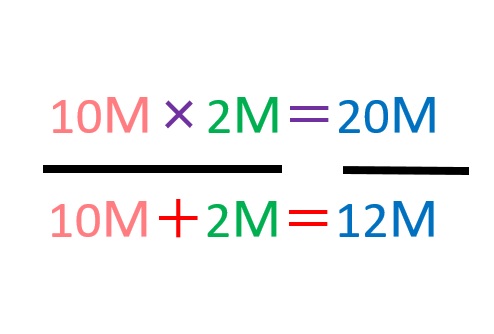
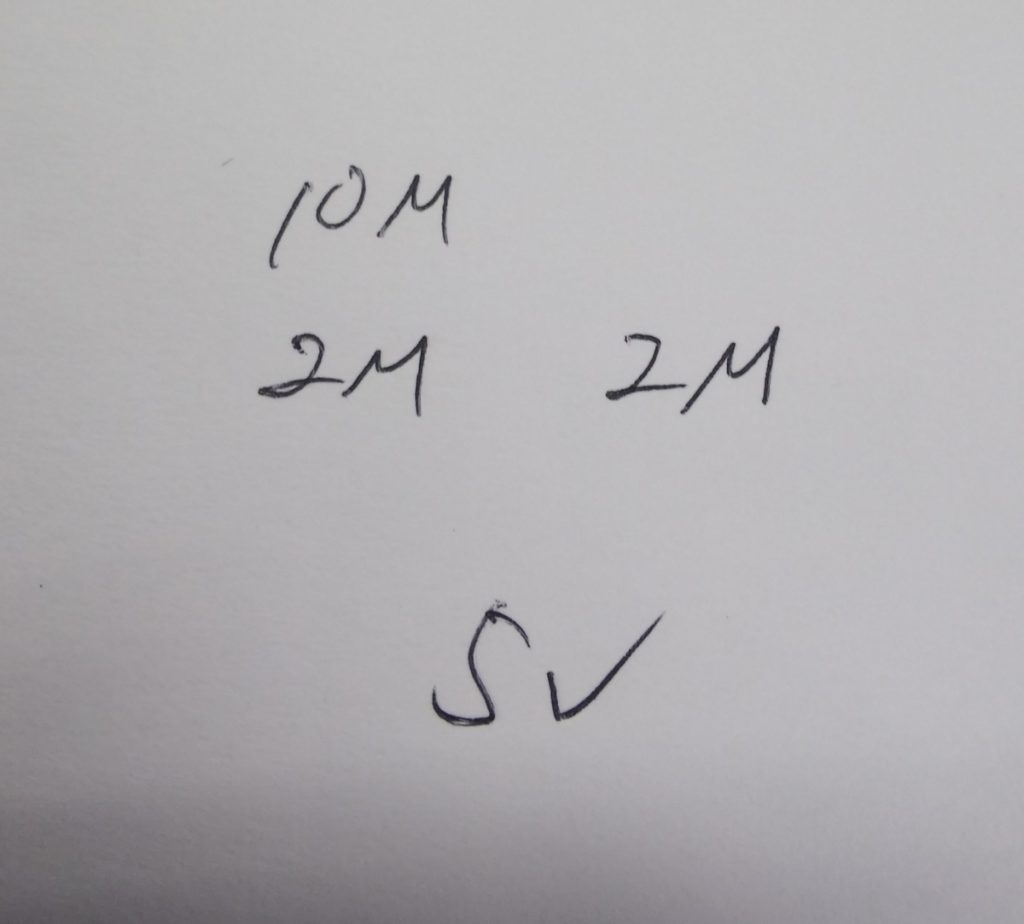
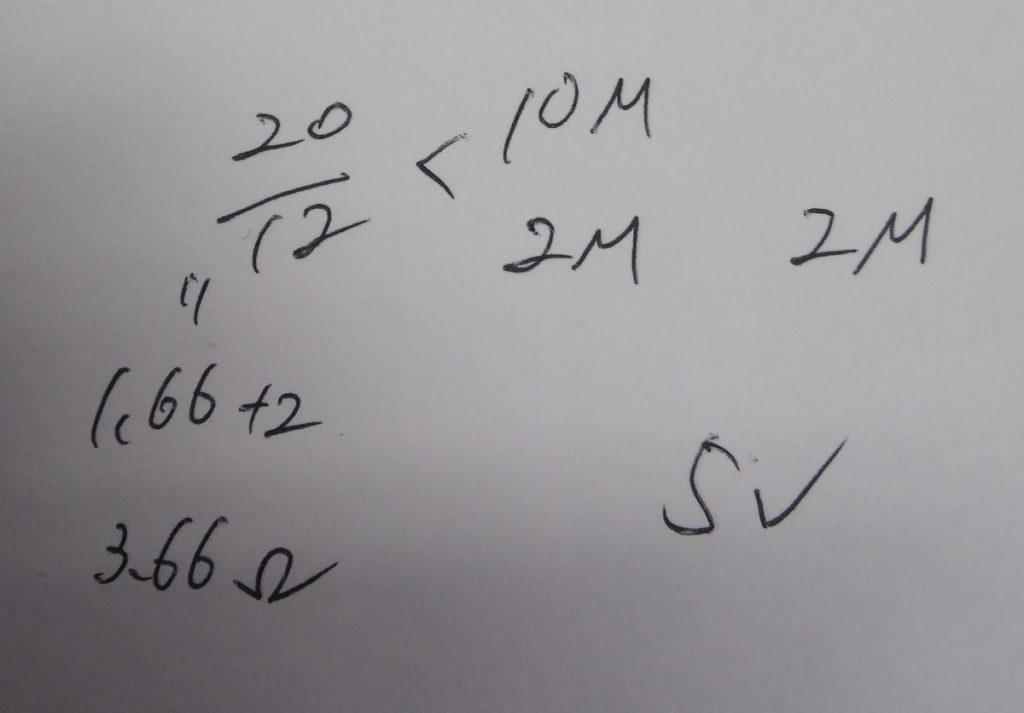


コメント